資訊熵
資訊量有方法量度嗎?當然有,一句十個字訊息跟一百字訊息所包含資訊當然大相逕庭。光看字數準確嗎?同一語言還可,然而不同語言不同字數所表達的 意思不同,本身基本上不可比。看檔案大小可以嗎?有時可以有時不可以,因為不同檔案類型大小不同,例如png通常比jpg要大得多,光看檔案大小並不準確。 因此,電腦科學中有一個數學方式表達資訊量,此概念就是資訊熵(Information Entropy)。
熵(粵音商)(entropy)原本是物理學的概念,代表的是事物混亂的程度:熵愈高,事愈亂。資訊理論(Information Theory)之父夏農(Claude Shannon)於1948 年將熵引入電腦科學,成為代表資訊量的量度,因此又名為夏農熵(Shannon)。
資訊熵的概念也很簡單,就是熵愈高,資訊愈多。也就是愈混亂,資訊愈多。
驟看之下,如此結論違反直覺,不是愈整齊愈多資訊嗎? 我們可以用以下簡單的例子,想像一下身處一個只有四個字母的世界,在左手邊Bucket 1中是清一色的A,中間Bucket 2有一半是A,Bucket 3則ABCD各 有二。

用資訊熵去量度,Bucket 3的資訊會最高,Bucket 2的資訊在中間, Bucket 1 的資訊最低。何解呢? 資訊熵量度的是,從Bucket中抽一個字母,平均需要多少條問題才可以判定該字母是A、B、C、D。
- Bucket 1全部都是A,如何抽都是A,一條問題也不需要,資訊熵自然是0。
- Bucket 2 有一半是A,一半不是A,約需要1.75條問題,所以資訊熵是1.75,詳情可以按此。
- Bucket 3 ABCD各有兩個,兩條問題可以造成四個可能,所以資訊熵是2。
由簡單角度看,Bucket 1最整齊,Bucket 3最混亂,根據愈混亂,資訊愈多原則,Bucket3最多資訊亦非常合理。
用一個非常生活化的例子去理解,剛買的硬碟就是Bucket 1,非常整齊,裝落資料的硬碟就像Bucket 3,資料孰多孰少就容易理解得多。
數學計算
當然作為一個數學概念,資訊熵不會流於表面,「吹水」而已。要計算資訊熵,須要用到所謂的夏農公式:
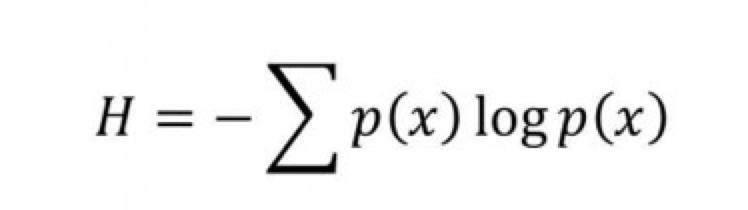
無學過數學,無須驚慌。其實很簡單,p(x) 其實就是相應字母的概率,假如有一條訊息只有廿六個英文字母,隨機抽取每一 個概率都是1/26. log其實即是ln,也就是自然對數,如果大家學過 e,也就是歐拉數的話,就知道ln(e) = 1,跟大家在學校學過的 log10(10) = 1 及 log10(100) = 2 一樣,只是底數不是10而是這個特別的e。
最後那個橫著的M ,就是Summation相加的意思,所以全條數學算式的意思就是如下:
每個字母的概率與其概率之自然對數相乘,再將每個字母的結果相加,相加之和的負數就是夏農熵。
知道理論後,大家可以這個網站嘗試計算不同字串的夏農熵, 例如如果你放入一句廿六個英母都有的句子: The quick brown fox jumps over the lazy dog.計算機計算出來的夏農熵將會是 4.39,也就是起碼需要五個位元才可以為此句編碼。
總結
常言道:電腦科學是資訊的科學,沒有資訊,也就沒了電腦科學。夏農熵作為電腦表達資訊量一個重要數學基礎,亦是由此開始了現代電腦的發展。
